For
it is based on the Chebyshev expansion
where
.
For
(see the
Users' Note for your implementation for value of
)
For
,
to within the representation accuracy of the machine and so this approximation is used.
None.
If
and
are the relative errors in the argument and the result respectively, then in principle,
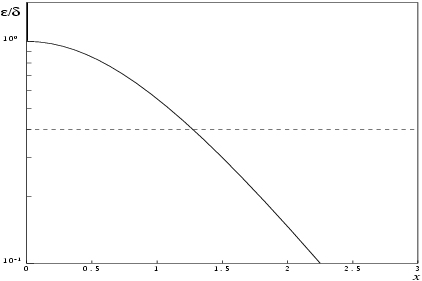
That is, a relative error in the argument,
, is amplified by a factor approximately
, in the result.
The behaviour of the amplification factor is shown in the following graph:
Figure 1
None.