None.
| (1) |
Open in the MATLAB editor: d02tz_example
function d02tz_example fprintf('d02tz example results\n\n'); global alpha beta eps; % For communication with local functions % Initialize variables and arrays. neq = int64(1); nlbc = int64(1); nrbc = int64(1); ncol = int64(5); mmax = int64(2); m = int64([2]); tols = [1.0e-05]; % Set values for problem-specific physical parameters. alpha = -1/3; beta = 1/3; eps = 1e-3; % Set up the mesh. nmesh = int64(7); mxmesh = int64(50); % Set location of mesh points, and specify which are fixed. mesh = zeros(mxmesh, 1); ipmesh = zeros(mxmesh, 1, 'int64'); mesh(1:nmesh) = [0.0; 0.15; 0.3; 0.5; 0.7; 0.85; 1.0]; ipmesh(1:2:nmesh) = 1; ipmesh(2:2:nmesh) = 2; % Prepare to store results for plotting. xarray = zeros(1,1); yarray = zeros(1,2); % d02tv is a setup routine to be called prior to d02tk. [work, iwork, ifail] = d02tv( ... m, nlbc, nrbc, ncol, tols, nmesh, mesh, ipmesh); ncont = 2; % We run through the calculation ncont times with different parameter sets. for jcont = 1:ncont eps = 0.1*eps; fprintf('\n Tolerance = %8.1e, eps = %10.3e\n\n', tols(1), eps); % Call d02tk to solve BVP for this set of parameters. [work, iwork, ifail] = d02tk( ... @ffun, @fjac, @gafun, @gbfun, @gajac, ... @gbjac, @guess, work, iwork); % Call d02tz to extract mesh from solution. [nmesh, mesh, ipmesh, ermx, iermx, ijermx, ifail] = ... d02tz( ... mxmesh, work, iwork); % Output mesh results. fprintf(' Used a mesh of %d points\n', nmesh); fprintf(' Maximum error = %10.2e in interval %d for component %d\n\n',... ermx, iermx, ijermx); % Output solution, and store it for plotting. fprintf(' Solution and derivative at every second point:\n'); fprintf(' x u u''\n'); for imesh = 1:nmesh % Call d02ty to perform interpolation on the solution. [y, work, ifail] = d02ty( ... mesh(imesh), neq, mmax, work, iwork); if mod(imesh, 2) ~= 0 fprintf(' %8.4f %8.5f %8.5f\n', mesh(imesh), y(1,1), y(1,2)); end xarray(imesh) = mesh(imesh); yarray(imesh, :) = y(1, :); end % Plot results for this parameter set. if jcont==1 fig1 = figure; else fig2 = figure; end display_plot(xarray, yarray, eps) % Select mesh for next calculation. if jcont < ncont nmesh = (nmesh+1)/2; % d02tx allows the current solution to be used as an initial % approximation to the solution of a related problem. [work, iwork, ifail] = d02tx( ... nmesh, mesh, ipmesh, work, iwork); end end function [f] = ffun(x, y, neq, m) % Evaluate derivative functions (rhs of system of ODEs). global eps f = zeros(neq, 1); f(1) = (y(1,1) - y(1,1)*y(1,2))/eps; function [dfdy] = fjac(x, y, neq, m) % Evaluate Jacobians (partial derivatives of f). dfdy = zeros(neq, neq, 1); machep = x02aj; fac = sqrt(machep); for i = 1:neq yp(i,1:m(i)) = y(i,1:m(i)); end for i = 1:neq for j = 1:m(i) ptrb = max(100*machep, fac*abs(y(i,j))); yp(i,j) = y(i,j) + ptrb; f1 = ffun(x, yp, neq, m); yp(i,j) = y(i,j) - ptrb; f2 = ffun(x, yp, neq, m); dfdy(:,i,j) = 0.5*(f1- f2)/ptrb; yp(i,j) = y(i,j); end end function [ga] = gafun(ya, neq, m, nlbc) % Evaluate boundary conditions at left-hand end of range. global alpha beta ga = zeros(nlbc, 1); ga(1) = ya(1,1) - alpha; function [dgady] = gajac(ya, neq, m, nlbc) % Evaluate Jacobians (partial derivatives of ga). dgady = zeros(nlbc, neq, 2); dgady(1,1,1) = 1; function [gb] = gbfun(yb, neq, m, nrbc) % Evaluate boundary conditions at right-hand end of range. global alpha beta gb = zeros(nrbc, 1); gb(1) = yb(1,1) - beta; function [dgbdy] = gbjac(yb, neq, m, nrbc) % Evaluate Jacobians (partial derivatives of gb). dgbdy = zeros(nrbc, neq, 2); dgbdy(1,1,1) = 1; function [y, dym] = guess(x, neq, m) % Evaluate initial approximations to solution components and derivatives. global alpha beta y = zeros(neq, 2); dym = zeros(neq, 1); y(1,1) = alpha + (beta - alpha)*x; y(1,2) = beta - alpha; dym(1) = 0; function display_plot(x, y, eps) % Plot the results. [haxes, hline1, hline2] = plotyy(x, y(:,1), x, y(:,2)); % Set the axis limits and the tick specifications to beautify the plot. set(haxes(1), 'YLim', [-0.5 0.5]); set(haxes(1), 'YMinorTick', 'on'); set(haxes(1), 'YTick', [-0.5 -0.25 0 0.25 0.5]); set(haxes(2), 'YLim', [0 2]); set(haxes(2), 'YTick', [0 0.25 0.5 0.75 1.0 1.25 1.5 1.75 2]); set(haxes(2), 'YMinorTick', 'on'); for iaxis = 1:2 % These properties must be the same for both sets of axes. set(haxes(iaxis), 'XLim', [0 1]); end set(gca, 'box', 'off') % Add title. title('Largerstrom-Cole Equation (-1/3, 1/3)'); text(0.4,0.4,['eps = ', num2str(eps)]); % Label the axes. xlabel('x'); ylabel(haxes(1), 'Solution'); ylabel(haxes(2), 'Derivative'); % Add a legend. legend('solution','derivative','Location','Best'); % Set some features of the three lines. set(hline1, 'Linewidth', 0.25, 'Marker', '+', 'LineStyle', '-'); set(hline2, 'Linewidth', 0.25, 'Marker', 'x', 'LineStyle', '--');
d02tz example results
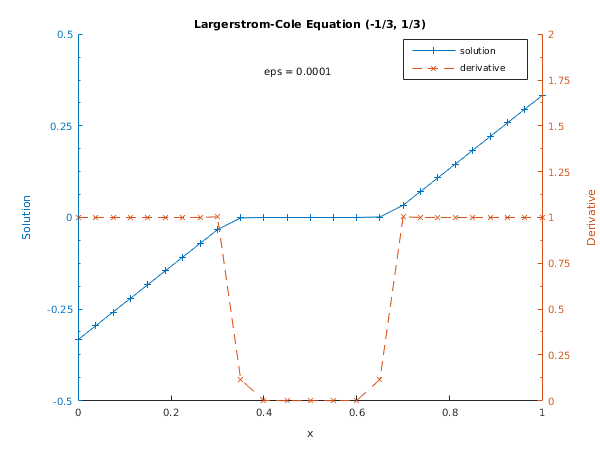
Tolerance = 1.0e-05, eps = 1.000e-04
Used a mesh of 25 points
Maximum error = 2.15e-06 in interval 16 for component 1
Solution and derivative at every second point:
x u u'
0.0000 -0.33333 1.00000
0.0750 -0.25833 1.00000
0.1500 -0.18333 1.00000
0.2250 -0.10833 1.00002
0.3000 -0.03332 1.00372
0.4000 -0.00001 0.00084
0.5000 -0.00000 0.00000
0.6000 0.00001 0.00084
0.7000 0.03332 1.00372
0.7750 0.10833 1.00002
0.8500 0.18333 1.00000
0.9250 0.25833 1.00000
1.0000 0.33333 1.00000
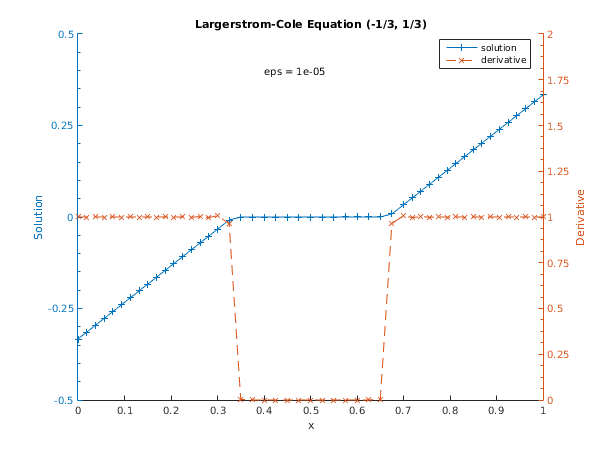
Tolerance = 1.0e-05, eps = 1.000e-05
Used a mesh of 49 points
Maximum error = 2.11e-06 in interval 32 for component 1
Solution and derivative at every second point:
x u u'
0.0000 -0.33333 1.00014
0.0375 -0.29583 1.00018
0.0750 -0.25833 1.00022
0.1125 -0.22083 1.00029
0.1500 -0.18333 1.00040
0.1875 -0.14583 1.00059
0.2250 -0.10833 1.00098
0.2625 -0.07083 1.00202
0.3000 -0.03333 1.00745
0.3500 -0.00001 0.00354
0.4000 -0.00000 0.00000
0.4500 -0.00000 0.00000
0.5000 0.00000 -0.00000
0.5500 0.00000 0.00000
0.6000 0.00000 0.00000
0.6500 0.00001 0.00354
0.7000 0.03333 1.00745
0.7375 0.07083 1.00202
0.7750 0.10833 1.00098
0.8125 0.14583 1.00059
0.8500 0.18333 1.00040
0.8875 0.22083 1.00029
0.9250 0.25833 1.00022
0.9625 0.29583 1.00018
1.0000 0.33333 1.00014