NAG C Library Function Document
nag_bessel_k0_vector (s18aqc)
1
Purpose
nag_bessel_k0_vector (s18aqc) returns an array of values of the modified Bessel function .
2
Specification
| #include <nag.h> |
| #include <nags.h> |
| void |
nag_bessel_k0_vector (Integer n,
const double x[],
double f[],
Integer ivalid[],
NagError *fail) |
|
3
Description
nag_bessel_k0_vector (s18aqc) evaluates an approximation to the modified Bessel function of the second kind for an array of arguments , for .
Note: is undefined for and the function will fail for such arguments.
The function is based on five Chebyshev expansions:
For
,
For
,
For
,
For
,
For
near zero,
, where
denotes Euler's constant. This approximation is used when
is sufficiently small for the result to be correct to
machine precision.
For large , where there is a danger of underflow due to the smallness of , the result is set exactly to zero.
4
References
5
Arguments
- 1:
– IntegerInput
-
On entry: , the number of points.
Constraint:
.
- 2:
– const doubleInput
-
On entry: the argument of the function, for .
Constraint:
, for .
- 3:
– doubleOutput
-
On exit: , the function values.
- 4:
– IntegerOutput
-
On exit:
contains the error code for
, for
.
- No error.
- , is undefined. contains .
- 5:
– NagError *Input/Output
-
The NAG error argument (see
Section 3.7 in How to Use the NAG Library and its Documentation).
6
Error Indicators and Warnings
- NE_ALLOC_FAIL
-
Dynamic memory allocation failed.
See
Section 2.3.1.2 in How to Use the NAG Library and its Documentation for further information.
- NE_BAD_PARAM
-
On entry, argument had an illegal value.
- NE_INT
-
On entry, .
Constraint: .
- NE_INTERNAL_ERROR
-
An internal error has occurred in this function. Check the function call and any array sizes. If the call is correct then please contact
NAG for assistance.
See
Section 2.7.6 in How to Use the NAG Library and its Documentation for further information.
- NE_NO_LICENCE
-
Your licence key may have expired or may not have been installed correctly.
See
Section 2.7.5 in How to Use the NAG Library and its Documentation for further information.
- NW_IVALID
-
On entry, at least one value of
x was invalid.
Check
ivalid for more information.
7
Accuracy
Let and be the relative errors in the argument and result respectively.
If
is somewhat larger than the
machine precision (i.e., if
is due to data errors etc.), then
and
are approximately related by:
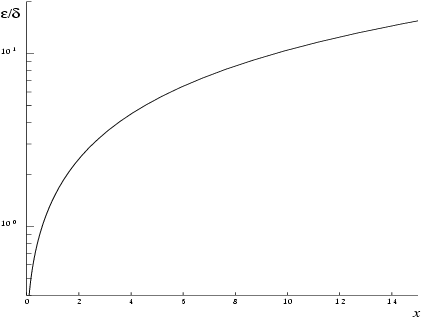
Figure 1 shows the behaviour of the error amplification factor
However, if is of the same order as machine precision, then rounding errors could make slightly larger than the above relation predicts.
For small , the amplification factor is approximately
, which implies strong attenuation of the error, but in general can never be less than the machine precision.
For large , and we have strong amplification of the relative error. Eventually , which is asymptotically given by , becomes so small that it cannot be calculated without underflow and hence the function will return zero. Note that for large the errors will be dominated by those of the standard function exp.
8
Parallelism and Performance
nag_bessel_k0_vector (s18aqc) is not threaded in any implementation.
None.
10
Example
This example reads values of
x from a file, evaluates the function at each value of
and prints the results.
10.1
Program Text
Program Text (s18aqce.c)
10.2
Program Data
Program Data (s18aqce.d)
10.3
Program Results
Program Results (s18aqce.r)