NAG Library Routine Document
C05BBF
1 Purpose
C05BBF computes the values of Lambert's function .
2 Specification
| INTEGER |
BRANCH, IFAIL |
| REAL (KIND=nag_wp) |
RESID |
| COMPLEX (KIND=nag_wp) |
Z, W |
| LOGICAL |
OFFSET |
|
3 Description
C05BBF calculates an approximate value for Lambert's
function (sometimes known as the ‘product log’ or ‘Omega’ function), which is the inverse function of
The function
is many-to-one, and so, except at
,
is multivalued. C05BBF allows you to specify the branch of
on which you would like the results to lie by using the parameter
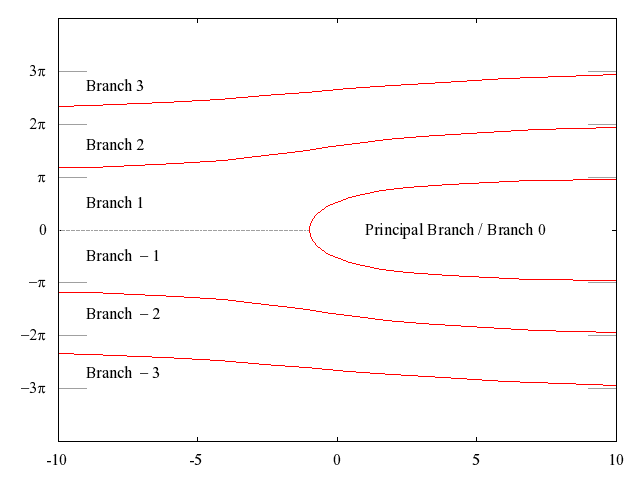
BRANCH. Our choice of branch cuts is as in
Corless et al. (1996), and the ranges of the branches of
are summarised in
Figure 1.
Figure 1: Ranges of the branches of
For more information about the closure of each branch, which is not displayed in
Figure 1, see
Corless et al. (1996). The dotted lines in the Figure denote the asymptotic boundaries of the branches, at multiples of
.
The precise method used to approximate
is as described in
Corless et al. (1996). For
close to
greater accuracy comes from evaluating
rather than
: by setting
on entry you inform C05BBF that you are providing
, not
, in
Z.
4 References
Corless R M, Gonnet G H, Hare D E G, Jeffrey D J and Knuth D
E (1996) On the Lambert function Advances in Comp. Math. 3 329–359
5 Parameters
- 1: BRANCH – INTEGERInput
On entry: the branch required.
- 2: OFFSET – LOGICALInput
On entry: controls whether or not
Z is being specified as an offset from
.
- 3: Z – COMPLEX (KIND=nag_wp)Input
On entry: if
,
Z is the offset
from
of the intended argument to
; that is,
is computed, where
.
If
,
Z is the argument
of the function; that is,
is computed, where
.
- 4: W – COMPLEX (KIND=nag_wp)Output
On exit: the value
: see also the description of
Z.
- 5: RESID – REAL (KIND=nag_wp)Output
On exit: the residual
: see also the description of
Z.
- 6: IFAIL – INTEGERInput/Output
-
On entry:
IFAIL must be set to
,
. If you are unfamiliar with this parameter you should refer to
Section 3.3 in the Essential Introduction for details.
For environments where it might be inappropriate to halt program execution when an error is detected, the value
is recommended. If the output of error messages is undesirable, then the value
is recommended. Otherwise, because for this routine the values of the output parameters may be useful even if
on exit, the recommended value is
.
When the value is used it is essential to test the value of IFAIL on exit.
On exit:
unless the routine detects an error or a warning has been flagged (see
Section 6).
6 Error Indicators and Warnings
If on entry
or
, explanatory error messages are output on the current error message unit (as defined by
X04AAF).
Note: C05BBF may return useful information for one or more of the following detected errors or warnings.
Errors or warnings detected by the routine:
Warning: the actual argument to was very close to . If or on entry, the output message provides more details of the nature of the warning.
Warning: the iterative procedure used internally did not appear to be converging. Check the value of
RESID for the accuracy of
W.
7 Accuracy
For a high percentage of
, C05BBF is accurate to the number of decimal digits of precision on the host machine (see
X02BEF). An extra digit may be lost on some platforms and for a small proportion of
. This depends on the accuracy of the base-
logarithm on your system.
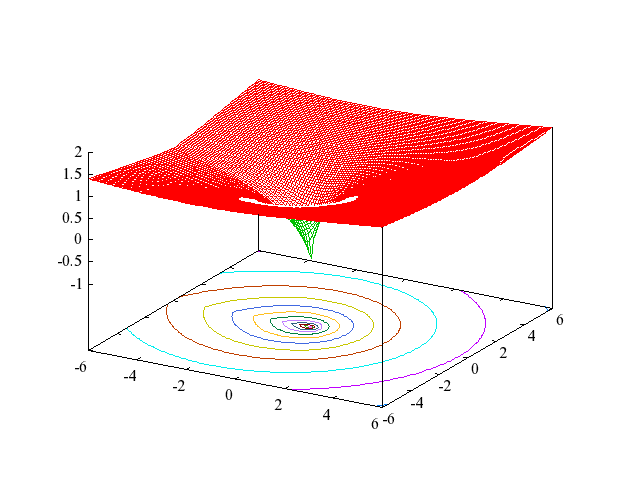
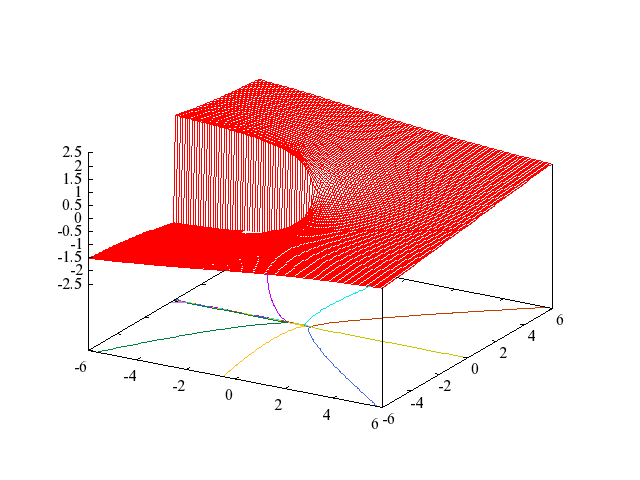
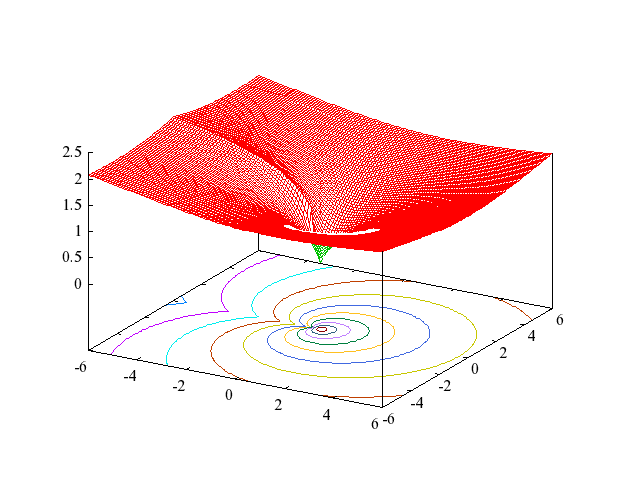
The following figures show the principal branch of
.
Figure 2:
Figure 3:
Figure 4:
9 Example
This example reads from a file the value of the required branch, whether or not the arguments to are to be considered as offsets to , and the arguments themselves. It then evaluates the function for these sets of input data and prints the results.
9.1 Program Text
Program Text (c05bbfe.f90)
9.2 Program Data
Program Data (c05bbfe.d)
9.3 Program Results
Program Results (c05bbfe.r)