NAG Library Chapter Introduction
c09 – Wavelet Transforms
1 Scope of the Chapter
This chapter is concerned with the analysis of datasets (or functions or operators) in terms of frequency and scale components using wavelet transforms. Wavelet transforms have been applied in many fields from time series analysis to image processing and the localization in either frequency or scale that they provide is useful for data compression or denoising. In general the standard wavelet transform uses dilation and scaling of a chosen function,
, (called the mother wavelet) such that
where
gives the scaling and
determines the translation. Wavelet methods can be divided into continuous transforms and discrete transforms. In the continuous case, the pair
and
are real numbers with
. For the discrete transform,
and
can be chosen as
,
for integers
,
The continuous real valued, one-dimensional wavelet transform (CWT) is included in this chapter. The discrete wavelet transform (DWT) at a single level together with its inverse and the multi-level DWT with inverse are also provided for one, two and three dimensions. The Maximal Overlap DWT (MODWT) together with its inverse and the multi-level MODWT with inverse are provided for one dimension. The choice of wavelet for CWT includes the Morlet wavelet and derivatives of a Gaussian while the DWT and MODWT offer the orthogonal wavelets of Daubechies and a selection of biorthogonal wavelets.
2 Background to the Problems
The CWT computes a time-frequency analysis of a signal,
, which can yield high localization in time of the high frequency features present. It is defined as
where
denotes the complex conjugate of the wavelet function,
is the dilation parameter and
is the localization parameter. (Currently only the real valued transform is offered.)
The discrete wavelet transform (DWT) is defined by a mother wavelet function
, and a related scaling function,
, where
These in turn are represented as a pair of filters with finite support. They can be viewed as a high pass filter,
, for
, paired with a low pass filter,
, for
. The DWT at a single level is carried out by convolution of the filter with the input data, followed by downsampling by two. The MODWT at a single level is carried out by convolution of the filter with the input data only; no downsampling is used in the MODWT. In order to obtain exact reconstruction of the original input these filters must satisfy certain conditions. For orthogonal wavelets,
, these are,
for all nonzero integers,
.
The DWT reconstruction algorithm convolves the inverse filters with the wavelet coefficients previously computed together with upsampling and summation to return to the original input. The MODWT reconstructs in the same way, except without upsampling. For orthogonal wavelets the inverse filters are the same as those for the forward DWT.
In the simplest case, the Haar wavelet, the nonzero filter coefficients are
while for the Daubechies wavelet with two vanishing moments and four nonzero coefficients, the filter coefficients are
In the orthogonal case the same filters are used for both decomposition and reconstruction.
Relaxing the orthogonality requirement allows for biorthogonal wavelets which consist of two dual wavelet bases. For example, the biorthogonal 2.2 filters are,
Note that there are several possible interpretations of orthogonal and biorthorgonal wavelet filters which satisfy the requirements. These differ in the sign of the coefficients and the ordering of the filters.
In order to obtain exact reconstruction when applying the DWT or MODWT and its inverse to a finite dataset, say , for , some method of extending the input at its end is required. Several methods which are in general use are: periodic extension, half-point symmetric extension, whole-point symmetric extension and zero end extension where the added data points are taken to be zero. The two types of symmetric end extension reflect the given data values from the end points for whole-point extension or else by repeating the end points and reflecting from points halfway between the end point and its repeat for half-point extension. Each of these end extension methods are available for the DWT. Only the periodic end extension is currently available for the MODWT.
2.1 Multiresolution and higher dimensional DWT
Rather than simply applying the wavelet transform at a single level the process is commonly repeated to give a multiresolution analysis. For the DWT, multiresolution is implemented as the pyramid (or cascade) algorithm. Applying the DWT at a given level, , the detail coefficients (which are the output from the high pass filter) are stored while the approximation coefficients resulting from convolution with the low pass filter are passed to the next level and the processs is repeated. When the length of the initial data input is an array of length , for some integer (and assuming that the dataset is extended by periodic repetition) this can be continued until, at level , there is a single detail coefficient from the high pass filter. The final coefficient from the action of the low pass filter is also stored. The result is an array of coefficients of the same length, , as the input.
For the multi-level MODWT it is, in theory, possible to continue for any number of levels. However, in practice it is common to not exceed levels in order to avoid scales that exceed the length of the input data, . This restriction is enforced for the one-dimensional mutli-level MODWT function in this chapter.
For two-dimensional data sets the DWT is computed as a series of one-dimensional DWTs, first over columns of the input data, and then over rows of the intermediate result. This produces four types of output coefficients: one set of approximation coefficients and three types of detail coefficients, containing information about the horizontal, vertical and diagonal components of the input data. The approximation coefficients are the result of applying convolution and downsampling with the low pass filter over both columns and rows;
the horizontal detail coefficients are the result of applying convolution and downsampling with the high pass filter over columns and then the low pass filter over rows; the vertical detail coefficients are the result of applying convolution and downsampling with the low pass filter over columns and the high pass filter over rows; and the diagonal detail coefficients are the result of applying convolution and downsampling with the high pass filter over both columns and rows. An example of the single level decomposition of an image performed using
nag_dwt_2d (c09eac) is given in
Figure 1.
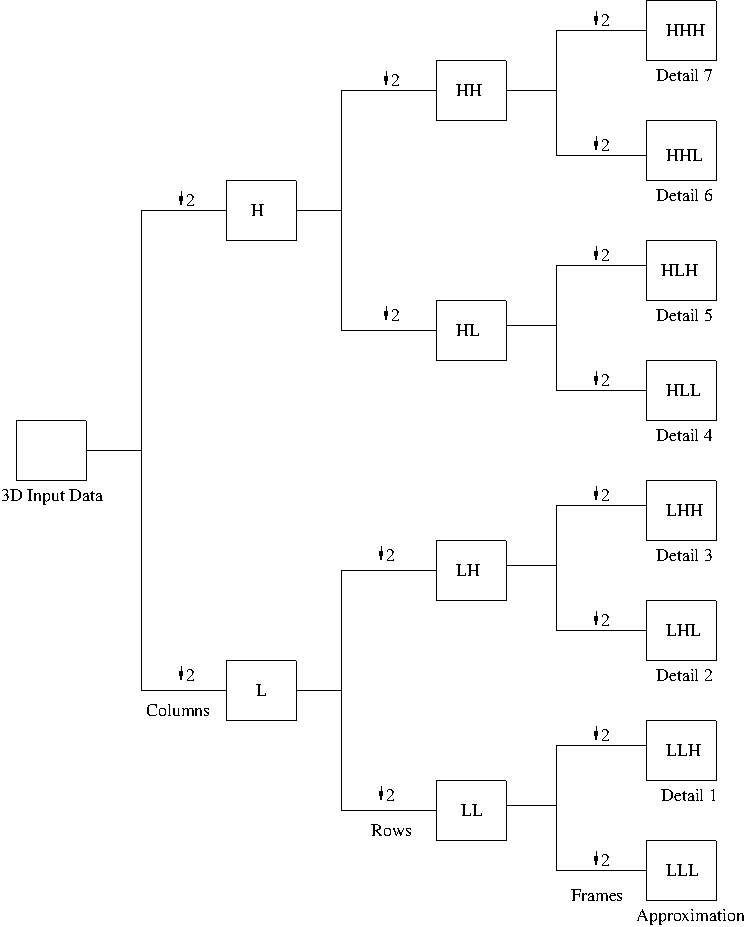
Similarly, for three-dimensional data sets the DWT is also computed as a series of three one-dimensional DWTs, first over columns of the input data, and then over rows of the intermediate result and finally over frames of the second intermediate result. This produces eight types of output coefficients: one set of approximation coefficients (labelled LLL since the low pass filter is applied over columns, rows and frames) and seven types of detail coefficients, labelled similarly according to whether the low pass (L) or high pass filter (H) is applied in each of the three dimensions.
For the three-dimensional DWT this process is represented by
Figure 2.
As in the one-dimensional case, the multi-level DWT in two and three dimensions is also implemented as the pyramid (or cascade) algorithm, where at a given level, , all detail coefficients are stored, while the approximation coefficients are passed as input to the next level.
Figure 2: The three-dimensional DWT filter bank. The original input is downsampled by and the high pass (H) and low pass (L) filters are applied along columns. This process is repeated along the rows and then frames to produce sets of output coefficients – one set of approximation coefficients and sets of detail coefficients.
3 Recommendations on Choice and Use of Available Functions
The one-dimensional real valued continuous wavelet transform is provided by
nag_cwt_1d_real (c09bac). It is useful for resolving discontinuities and high frequency features in a signal. It is a redundant representation of the input data containing repeated information and the set of coefficients produced as output is larger than the input data set.
The one-dimensional discrete wavelet transform at a single level is performed by
nag_dwt (c09cac). The inverse or reconstruction is carried out by
nag_idwt (c09cbc).
The one-dimensional multi-level discrete wavelet transform is computed by
nag_mldwt (c09ccc) and the inverse or reconstruction is given by
nag_imldwt (c09cdc). The discrete wavelet transform is widely used for image processing and data compression.
The one-dimensional maximal overlap discrete wavelet transform at a single level is performed by
nag_modwt (c09dac). The inverse or reconstruction is carried out by
nag_imodwt (c09dbc).
The one-dimensional multi-level maximal overlap discrete wavelet transform is performed by
nag_mlmodwt (c09dcc). The inverse or reconstruction routine is
nag_imlmodwt (c09ddc). The maximal overlap discrete wavelet transform overcomes the lack of translation invariance inherent in the DWT, and thus there are advantages to using the MODWT when carrying out multiresolution analysis.
nag_wfilt (c09aac) is provided to determine some of the input arguments for the one-dimensional discrete wavelet transform and maximal overlap discrete wavelet transform functions and must be called before the one-dimensional transform functions.
The two-dimensional discrete wavelet transform at a single level is performed by
nag_dwt_2d (c09eac). The inverse or reconstruction is carried out by
nag_idwt_2d (c09ebc).
The two-dimensional multi-level discrete wavelet transform is computed by
nag_mldwt_2d (c09ecc) and the inverse or reconstruction is given by
nag_imldwt_2d (c09edc).
nag_mldwt_2d (c09ecc) and
nag_imldwt_2d (c09edc) use a one-dimensional array to store the discrete wavelet transform coefficients. These may be extracted into two-dimensional arrays using
nag_wav_2d_coeff_ext (c09eyc). A complementary function
nag_wav_2d_coeff_ins (c09ezc) allows for the insertion of coefficients held in a two-dimensional array back into the one-dimensional array.
nag_wfilt_2d (c09abc) is provided to determine some of the input arguments for the two-dimensional discrete wavelet transform functions and must be called before the two-dimensional transform functions.
The three-dimensional discrete wavelet transform at a single level is performed by
nag_dwt_3d (c09fac). The inverse or reconstruction is carried out by
nag_idwt_3d (c09fbc).
The three-dimensional multi-level discrete wavelet transform is computed by
nag_mldwt_3d (c09fcc) and the inverse or reconstruction is given by
nag_imldwt_3d (c09fdc).
nag_dwt_3d (c09fac),
nag_idwt_3d (c09fbc),
nag_mldwt_3d (c09fcc) and
nag_imldwt_3d (c09fdc) use a one-dimensional array to store the discrete wavelet transform coefficients. These may be extracted into three-dimensional arrays using
nag_wav_3d_coeff_ext (c09fyc). A complementary function
nag_wav_3d_coeff_ins (c09fzc) allows for the insertion of coefficients held in a three-dimensional array back into the one-dimensional array.
nag_wfilt_3d (c09acc) is provided to determine some of the input parameters for the three-dimensional discrete wavelet transform functions and must be called before the three-dimensional transform functions.
4 Functionality Index
5 Auxiliary Functions Associated with Library Function Arguments
None.
6 Functions Withdrawn or Scheduled for Withdrawal
None.
7 References
Daubechies I (1992) Ten Lectures on Wavelets SIAM, Philadelphia
Mallat S G (1998) A Wavelet Tour of Signal Processing Academic Press
Percival D B and Walden A T (2000) Wavelet Methods for Time Series Analysis Cambridge University Press
Strang G and Nguyen T (1996) Wavelets and Filter Banks Wellesley-Cambridge Press
Vidakovic B (1999) Statistical Modeling by Wavelets John Wiley and Sons Inc.
Wickerhauser M V (1994) Adapted Wavelet Analysis from Theory to Software A K Peters Ltd